



|
akutek.info |
|
The www center for search, research and free sharing in acoustics |
|
Small Room Acoustics |
|
This page is dedicated to acoustics in smaller rooms for music, speech and other purposes that are sensitive to room acoustic properties of smaller rooms. What is a small room in terms of acoustics? In this context, a room is considered small if the acoustics of the room is dominated by the Modal Region, e.g. the frequency region where f<Fc, see below, or its use is sensitive to the acoustics in this region. Other significant features of smaller rooms are smaller absorption area and shorter reverberation time. For music rehearsals, small room size typically means that one cannot have the same acoustics as in a performance room, since by Sabine, T*A=0.16*V is constant for a given room. T is reverberation time, A absorption area, and V the volume of the room. In contrast to small room acoustics, the acoustics of a large room is dominated by stochastic processes, and not by single, separable modes. For frequencies higher than the absorption-dependent Schroeder Frequency Fc~2000·(T/V)1/2 ~800/A1/2 , where T is the reverberation time, V the volume in cubic meters, and A the total (Sabine) absorption area of the room, the reverberant sound field is dominated by conditions that can be predicted by geometrical acoustics (GA), e.g. with ray-tracing methods. This means that sound in many ways acts like light, only with slower propagation speed, and thus sound rays and sound particles can be helpful models in frequency domain and time domain respectively. In a 20.000 cubic meter hall with T~2.0s, the Schroeder frequency is 20Hz, so GA applies in the practical frequency range of most concert halls. Fc as a small room criterion. In small rooms, Fc is in the order of hundreds of Hertz, meaning that tones in music and speech fall in the Modal Region. Periodic reflections are in small rooms largely perceived as modes, affecting tonal response, while they in larger rooms are perceived as flutter-echoes, affecting temporal response, as illustrated in the Hard Case. In cuboids, every mode is the fundamental F in a harmonic spectrum forming a Fourier Transformation pair with a periodic reflection of period 1/T. Though often defined by the distance between parallel walls, reflection periods may have less obvious geometric explanation, making them hard to predict and hard to avoid. The Hard Case A cuboid room with hard surfaces except an absorbing ceiling, is both a common case and a difficult case, creating a 2-dimensional sound field that calls for control by diffusing elements that can redirect sound to the absorbing ceiling. While furniture and other obstacles may redirect low-frequency sound to the ceiling absorber, they may leave large open cross sections in upper half of the room. Taking care of medium- and high-frequency sound will require diffusers in all open cross-sections. Thus, wall-mounted diffusers are often the only practical solution. 2D sound field frequency limit Similar to the Schroeder Frequency, requiring minimum 3-fold modal overlap in the high-frequency range (large-room acoustics), the 2-dimensional sound field would in the horizontal case with floor area S have a limiting frequency expressed by Fc,2D ~ 12500*T/S where T is the reverberation time of the 2-dimensional sound field. AKUTEK article: Two-dimensional room acoustics. Slanted walls may eliminate some periodic modes, but then may allow some more hidden ones. This is demonstrated in the image room diagram below, see illustration series Figure 1-4. A hard plane wall act like an acoustic mirror so that reflections from the wall can be explained as coming from an image room behind the wall. Two walls meeting at a right angle will create three image rooms from where reflections appear to come from. As long as geometries are simple (close to cuboid rooms), the principle can be extended to reveal that the hidden mode or the flutter-echo can be explained as plane-wave reflections between two parallel surfaces in a cluster of image rooms. Related topics Rehearsal room acoustics, Echoes and Flutter-echoes, Voice Acoustics Small Room Acoustics - The Hard Case Forum Acusticum 2011 presentation by M Skålevik Small Room Acoustics - The Hard Case (full paper) Schroeder Frequency Revisited, Forum Acusticum 2011 presentation by M Skålevik Schroeder Frequency Revisited (full paper)
|
|
Acoustics in smaller rooms for music and speech |
|
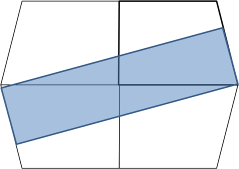
Fig 2. Image rooms with a wavefront and its image wavefronts travelling towards a right angle corner |
|
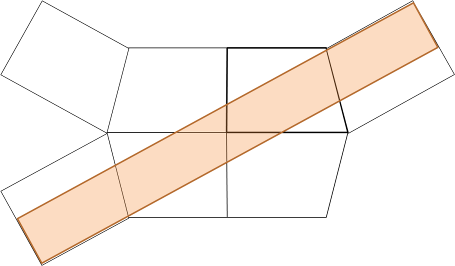
Fig 3. Image rooms, revealing hidden parallel walls, allowing a periodic mode, e.g. a flutter-echo. Slanting the wall does not resolve the parallel wall problem, it only alters the loop length, its period and its mode frequency. |
|
Fig 4. (above) Extended cluster of image rooms, revealing even more hidden parallel walls, allowing a flutter-echo of longer period than the one in Fig.3. Note that the loop length is about twice the one associated with an unslanted wall. (right) Folding the imaginary box in which the plane wave travels, into the real room, demonstrates how the right-angle corner throws back the plane wave, undistorted, via the slanted wall, toward its origin, thus satisfying the condition for any harmonic mode: Two plane waves travelling in opposite directions. |


|
Fig 1. Room with slanted wall |
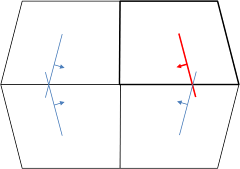
|
Slanted walls and periodic reflections between parallel image walls. An illustration. |
|
Small Room Acoustics History Since Bolt (1946) [1], in the aim for evenly spaced modes, came up with a method for determining preferable room ratios, researchers have continued to search for the optimum room dimensions based on various criteria. A review of papers in this special field of small room acoustics was given in a paper by Cox and D’Antonio[16] in 2004. Some highlights from research in small room acoustics in general in the period from the early 1940’s until present follows. The 2:3:5 ratio recommended by Volkman [1] becomes less supported as time goes by, and the same goes for Boner’s [2] 1:1.26:1.59 from the following pages of the same publication (1942). The importance of axial modes are pointed at by Gilford (1959) [6], who also reports from an interesting study of coloration in radio broadcasting studios, corresponding to frequencies in the range of 100-175Hz by male voices and 200-300Hz by female voices. Another development is the shift from studying average mode spacing to standard deviation of mode spacing, the latter being suggested as a single figure of merit by Louden[8] (1971). Bonello [11] differs from other authors by leaving the interest for mode spacing in favour of his own criterion of non-decreasing density of modes within increasing third-octave-bands (1981). Work by Walker [12][13] influence Broadcasting Union recommendations (1998), which as discussed by Walker leaves the golden ratios alone and rather aims at avoiding the worst cases. Cox and D’Antonio [16] presented a new approach in small room acoustic planning, aiming for the flattest possible frequency response (2000 and 2004). Cuboid rooms dominate in detailed studies of geometry and acoustic quality. Other geometries have been examined by finite element methods (FEM), but such studies have been few since they require high computational capacity. Results from Nieuwland [10] and Weber includes pressure amplitude contour plots of rooms with splayed walls compared with rooms with parallell walls. Splaying the walls apparently reduces pressure gradients, but it is not clear if it provides less area having peaks and dips and reduced standard deviation of levels in the average receiver point. At least 5% splaying of walls is necessary to have an effect on degeneracy of modes [15]. Thumb rules of 6 to 12 degrees deviation from parallell have been common, but strangely enough not related to distance between such wall pairs. This author has suggested that splaying or other deviation from parallell should be related to distance between wall pairs [18], since one and the same degree of slanting is expected to have larger effect on a standing wave if wall distance was shorter. Sommerville and Ward (1951) reported that geometrical diffusing elements reduced fluctuations in a swept-sine steady-state transmission test. For a noticeable effect, such geometrical diffusors had to be at least 1/7 of a wavelength, and in their study of cylindrical, triangular and rectangular elements, the rectangular shape proved the more effective for both steady-state and transient phenomena. Splaying one or two walls may improve diffusion, but does not eliminate modal problems[5]. Geometries deviating from rectangular sections (slanted walls, etc) does not make coloration dissapear, only harder to predict, Gilford 1972) [9]. References 1. J.E.Volkman, ”Polycylindrical Diffusers in Room Acoustical Design”, J.Acous.Soc.Am., 13 (July 1942), p 234-243. 2. C.P.Boner, ”Performance of Broadcast Studios Designed with Convex Surfaces of Plywood”, J.Acous.Soc.Am., 13 (July 1942), p 244-247. 3. R. H. Bolt, “Note on The Normal Frequency Statistics in Rectangular Rooms,” J. Acoust. Soc. Am., vol. 18, pp. 130–133 (1946). 4. T.Sommerwille, F.L.Ward, ”Investigations of Sound Diffusion in Rooms by means of a Model”, 5. Nimura, Tadamoto and Kimio Shibayama, ”Effect of Splayed Walls of a Room on Steaty-State Sound Transmission Characteristics”, J.Acoust.Soc.Am., 29,1 (January 1957), p85-93. 6. C. L. S. Gilford, “The Acoustic Design of Talk Studios and Listening Rooms, 1959, reprinted in “J. Audio. Eng. Soc., vol. 27, pp. 17–31 (1979 Jan./Feb.). 7. M. R. Schroeder and K. H. Kuttruff, ‘‘On Frequency Response Curves in Rooms. Comparison of Experimental, Theoretical, and Monte Carlo Results for the Average Frequency Spacing between Maxima,’’ J. Acoust. Soc. Am. 34, 76–80 1962. 8. M. M. Louden, “Dimension Ratios of Rectangular Rooms with Good Distribution of Eigentones,” Acustica, vol. 24, pp. 101–104 (1971). 9. C.L.S.Gilford, ”Acoustics for Radio and Television Studios”, (1972), London, Peter Peregrinus Ltd. 10. J.M. van Nieuwland and C.Weber, ”Eigenmodes in Non-Rectangular Reverberation Rooms”, Noise Control Eng., 13, 3 (Nov/Dec 1979), 112-121. 11. O. J. Bonello, “A New Criterion for the Distribution of Normal Room Modes, “J. Audio. Eng. Soc., vol. 29, pp. 597–606 (1981 Sept.); Erratum, ibid., p. 905 (1981 Dec.). 12. R. Walker, “Optimum Dimension Ratios for Small Rooms,” presented of the 100th Convention of the Audio Engineering Society, J. Audio Eng. Soc. (Abstracts), vol. 44, p. 639 (1996 July/Aug.), preprint 4191. 13. R. Walker, “A Controlled-Reflection Listening Room for Multichannel Sound,” Proc. Inst. Acoust. (UK),vol. 20, no. 5, pp. 25–36 (1998). 14. EBU R22-1998, “Listening Conditions for the Assessment of Sound Programme Material,” Tech. Recommendation, European Broadcasting Union (1998). 15. F. A. Everest, ”The Master Handbook of Acoustics”, 4th ed., McGraw-Hill, New York, 2001, 16. T.Cox, P.D’Antonio, M.R.Avis, “Room Sizing and Optimization at Low Frequencies”, J. Audio Eng. Soc., Vol. 52, No. 6, 2004 June. 17. M.Skålevik, ”Schroeder Frequency Revisited”, Forum Acusticum 2011, Aalborg. 18. http://akutek.info/demo_files/rehearsal_room.htm 19. http://akutek.info/articles_files/stochastics.htm 20. http://www.acoustics.salford.ac.uk/res/cox/book/
Small room acoustics in AKUTEK article section: |
|
on site |