Reverberation distance in ensemble rehearsal rooms

Ensemble room acoustics

www.akutek.info

HOME

INDEX

Go to www.akutek.info main page Go to article site index page

This article is a living research report, to be continued and updated.

Reverberation distance - is it a critical property in orchestra acoustics?

Introduction

In ensembles, musicians and conductors hear a mix of direct and reverberant sound from several instruments. While the direct sound component is considered important when it comes to hearing details in the music, the reverberant sound component is important for the hearing of the blended unison sound from the first violins or other instrument groups.

From text books, the distance from a source at which direct sound and reverberant sound is equally strong is termed the reverberation distance, or the critical distance. Beyond the critical distance from an instrument, a co-musician or a conductor would hear the instrument via reverberant sound. If the ensemble moves to a room with different critical distance, their mutual hearing would be different. A common saying is that conductors like to hear details during the rehearsal phase, while in performance a more blended sound is preferred. This would imply a longer critical distance in the rehearsal room than in the performance room. This rarely is the case. However, some orchestras prefer to rehearse in far dryer rehearsal rooms than recommended by the standard NS8178.

This paradox is pursued in this article. Could it be they prefer the longer critical distance?

Problem

The problem under investigation is: Can the ratio V/T between V and reverberation time T provide more explanation as to why some ensemble and orchestra rehearsal rooms are preferred over others? In particular, can V/T explain why some orchestras with variable acoustics in their rehearsal rooms, after testing the options, choose the driest possible acoustics, instead of a reverberation time that are within the tolerance of the music room standard NS8178? Moreover, are adequate loudness and adequate acoustical transparency two sides of the same coin, controlled by V/T?

Relevance

The problem is generally relevant in the task of planning rehearsal rooms for ensembles and orchestras of different kinds. In particular, it is relevant in the discussion of determining adequate criteria in the ISO-standard for rehearsal room acoustics. Since a wish for good acoustic conditions for music ensembles is not restricted to the rehearsal rooms, the problem and possible solutions would be relevant to the performance conditions, i.e. the field of stage acoustic.

Features of study

Critical acoustic properties of a rehearsal room, in particular those related to T, V and T/V are studied.

Since reverberation time T alone does not provide a criterion for preferred rehearsal room acoustics, several other acoustical parameters and perceptive aspects have been explored by researchers and authors. The need for more volume V in rehearsal rooms have often been noted by authors. However, V is often restricted because of its implications on building costs and architectural concerns.

Features depending on V/T

Strength of reverberant sound

The ratio V/T is related to several basic properties in music rehearsal rooms. One of them is the reverberant loudness, or the reflected sound level, Gr, as described by Barron’s Revised Theory.

Gr= 45-10*lg(V/T)-0.176r/T

For the average inter-orchestral distances r in a typical rehearsal room, the latter term will be approximately 1dB, so a good estimate would be 44dB-10*log(V/T), demonstrating the dependence on V/T alone.

In order to limit the loudness during rehearsals, e.g. to prevent sound during rehearsals from being significantly louder than in the performance case, Gr in the rehearsal room should not be much higher than Gr in the performance situation. This could be controlled by comparison with simulated or measured Gr on the stage of the preferred performance room, assuming such preference is established. However, the reference “preferred performance room” would vary, depending on the type of ensemble and music.

Reverberant sound level balance

Another way to express the loudness concern, is to make sure that there is a balance between the direct sound from the ensemble and the reflected sound from the ensemble. This would mean a proper average balance between Gr and the direct sound component Gd=20-20log(r), within the ensemble. The direct-to-reverberant balance D-R is a much-used parameter in sound engineering, but less so in music room acoustics. D-R=Gd-Gr. Once a general value for the “proper balance” of average D-R is established, this would be a criterion that is independent of the varying reference mentioned before, the preferred performance room.

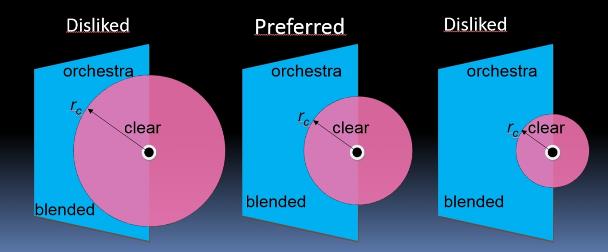
In a case study by Skalevik (IOA, Hamburg 2018), an orchestra with experience from various venues with average D-R varying between 3dB and -6dB clearly preferred venues where the average D-R was close to zero, when simulated in Odeon 14. Their preference correlated more with average D-R than any other of the many common parameters that was tested in the study. It was hypothesized that average(D-R)=0 dB at Conductor or Concertmaster’s position indicated a proper balance when simulated in occupied condition. One interpretation of this result is that the orchestra preferred the level of reflected sound from the orchestra to be equal to the level of non-reflected, i.e. direct or an-echoic, sound from the orchestra, Fig.1. As an implication, the musicians would receive sound from their co-musicians that were 3dB louder than it would be in an-echoic conditions. In this manner, sound exposure levels would at large be determined by the sound they produce, and not by the room. The criterion average(D-R)=0 dB is to be tested on more cases in future work.

Fig 1. From inside the critical radius rc, D-R>0dB and sound is direct and clear, while from outside D-R<0dB and sound is indirect and blended. The orchestra preferred an overall balance between clear and blended sound, i.e. average(D-R)≈0.

Reverberation Distance

In classical theory D-R occur at the source-receiver distance r=RD, where RD is the Reverberation Distance, or Hallradius rh, as defined in textbooks, e.g. Cremer & Müller, Kuttruff, and others. From their definitions, RD=0.057*(V/T)^0.5. It is expected that in cases where average D-R=0, RD would be close to the average inter-orchestral distance, and in particular, close to the average distance between conductor (or concertmaster) and the average musician. Ensembles would try to minimize the distance between musician and the conductor, and naturally form a layout that can be estimated by a semi-circular surface with radius Re related to the conductor (or concertmaster) position. Distances from instruments to conductor would be in the range of [0,Re], and D-R measured at conductor’s position, from instruments at distances around midway to the farthest instrument, i.e. around r=0.5*Re from the conductor.

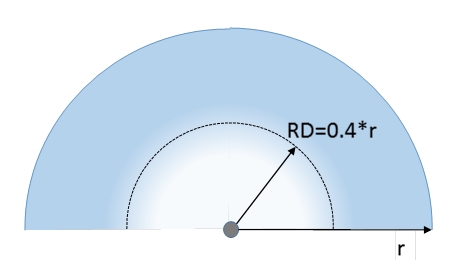
Sound exposure management by empirical data

Gade (Hong Kong, 2012) showed that among many orchestra rehearsal rooms, those with absorption area A of 8m2Sa per musician or more were well-liked and were preferred over the other ones. The criterion being A/N>8, when N is the number of musicians. This criterion is equivalent to V/T>50*N, V/N>50*T, and V/TN>50. An ensemble with a mix of instruments like a symphony orchestra would require a minimum floor space S/N of on average approximately 1.5m2 per musician. This ratio relates N to the geometrical size S. It can be shown V/TN>50 is equivalent to having a reverberation distance of RD>0.4*Re, Fig 2, which is comparable to the result r=0.5*Re above. Gade suggested the criterion with the purpose to protect musicians against excess noise exposure by compensating a varying number of sound sources by proportional variation of sound absorption and damping.

Fig 2. Reverberation distance from conductor of orchestra in a semi-circular layout with 1.5m2 per musician N and V/T=50*N

The A/N>8 criterion is well substantiated for symphony orchestra rehearsal rooms based on Gade’s empirical data. While the criterion would work well as long as the average source power was constant while the number of sources varied, it cannot without further be extrapolated to ensemble types with different average source power. For instance, the average source power of a brass band would be higher than the average source power in a symphony orchestra, in a string ensemble, or in a choir with untrained singers. Thus, as far as noise exposure protection is concerned, the brass band might consider using more absorption than the number of musicians would indicate. In this case, it would be safer to apply some of the other approaches described above. Note that the aim here is not to equalize natural variations between listening levels of different music styles. Idiomatic listening levels is a characteristic property of music types, styles or genre. Some music styles are meant to be loud at listener’s ears. Other styles can be softer by the composer’s intention, and it would be wrong to alter the listening level with room acoustical means.

Transparency

An important feature in ensemble room acoustics, is Acoustical Transparency, AT, or just transparency, i.e. the degree to which direct sound can be heard, as opposed to being masked, in the presence of reflected sound. We suggest AT is the average D-R+L(bin), where L(bin) is a hypothetical impact from binaural properties of the reverberant sound. However, L(bin) is not yet explored and quantified. In this paper, transparency will be simplified to AT=average(D-R).

Transparency is limited by reverberation distance RD in analogy to visual range or sight range, e.g. in meteorology, navigation, aviation, and road traffic. If fog or mist is more dense, visual range is shorter. In similar manner, if the reverberant sound field is denser, i.e. Gr is higher, the reverberation distance is shorter, meaning that direct sound is more masked and the task of discerning sources (the cocktail-party effect) becomes more difficult, Fig 3. Opposed to visual range, RD should not be too long, since this would be at the expense of desired blend offered by a proper amount of reverberant sound. The optimum RD would be related to the average inter-orchestral, i.e. the between-musicians distance, and the average conductor-to-musician distance, thus related to the size of the occupied floor space S of the given ensemble. Since S/N is a statistical characteristic for given types of ensembles, RD relates to N when S/N is given.

Fig 3. Analogy between acoustical transparency and visual range, the analogy between sight and hearing

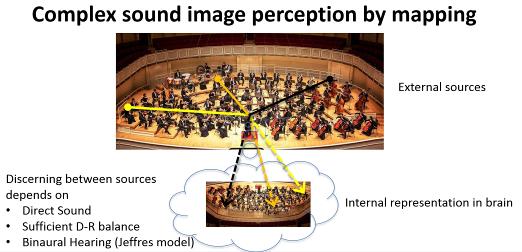
Cocktail-party effect

The brain in musicians and conductors relies on transparency combined with binaural hearing in the task of discerning between individual instruments, Fig 4, an ability known as the cocktail-party-effect, another important feature in ensemble room acoustics.

Fig 4. Binaural hearing allows external sources in a transparent sound field to be mapped by internal representation in brain

Escalating sound power due to inadequate reverb level

In the long run, a musician needs to hear one’s own instrument. If an orchestra would try to rehearse the exact same music, with the same conductor, in two different rooms—one with higher Gr than the other—the level balance between the musician’s own instrument and the total sound level would be lower in the room with higher Gr. When the self-to-total balance is weaker, “self” will be more masked by “total”. As Gr increases, masking will be more problematic.

Excess reverb in the orchestra rehearsal room may introduce a viscious circle. More reverberant sound from the whole orchestra may mask more of the sound from a musicians own instrument. Over time, the musician may compensate for this by playing a little bit stronger. However, when many, or all, musicians plays a little bit stronger, there will be a higher sound level and even more masking to compensate for. Moreover, at higher sound levels, masking is more effective, worsening the initial problem even more. On the other hand, too weak reverb in the orchestra rehearsal room may over time lead to musicians playing stronger, adopting a forced style of playing in order to compensate for lack of loudness. In order to avoid any of the two extremes, an optimum balance between reflected and non-reflected sound must be found. Again the key is to find the optimum balance of average(D-R) , in other words to find the optimum Reverberation Distance and optimum ratio V/T.

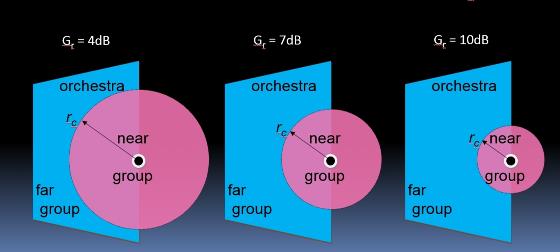
Entangled features

From the discussion of features above, it is interesting to note that attempts to control Gr leads to a certain D-R balance, and vice versa, Fig 5. This mutual dependence is to be expected from the fact that Gr and D-R both depend on V/T, as described above, and indicates that Acoustical Transparency and Loudness Control are two sides of the same coin, they are apparently entangled. In other words, Gr and D-R both depend on RD, meaning that reverberation distance indeed is a critical property in ensemble rehearsal room acoustics. However, V/T, the square relative of RD, is a more convenient parameter when it comes to establishing target values.

Fig 5. Reverberation distance and reverberant level are entangled

Frequency dependency

Generally, the features and parameters discussed in this paper are varying also with frequency. Directivity of musical instruments and sound transmission through an ensemble varies in general with frequency. However, mid-frequency sound is considered of special importance. Binaural hearing and depend very much on conditions in the mid-frequency region 300Hz-1500Hz, i.e. the octave bands 500 and 1000Hz. Criteria for low-frequency sound and high-frequency sound may both differ from criteria for mid-frequency sound.

Methodology

Basically, the problem can be expressed by the hypothesis that the important features in ensemble rehearsal acoustics are related to the ratio V/T and the number of musicians, N. The hypothesis will be tested by empirical data of V, T and N from preferred rooms as well as less preferred rooms for ensemble rehearsals. The interrelation between loudness and transparency will be investigated in simulations in a 3D model in Odeon.

Expected results and findings

It is expected to find that for a rehearsal room for a symphony orchestra to be well-liked, the V/T should be at least 50*N, equivalent to the volume per musician requirement V/N of at least 50*T. Moreover, it is expected that acoustical transparency D-R=0 dB coincide closely with V/T=50*N. Deviations from the critical V/T ratio is expected to be at the expense of either too loud reverb combined with too low transparency, or too weak reverb combined with too high transparency, i.e. too little blend in the ensemble sound.

The observation that some orchestras prefer to rehearse in dryer acoustics than those recommended by the standard NS8178, can be explained by the fact that the dryer acoustics offer better transparency and better balance between direct and reverberant sound, i.e. average(D-R) = 0dB.

Expected conclusions, applications and limitations

To the question posed in the title, RD is a critical property in ensemble rehearsal room acoustics. If RD is too small, transparency will be too low and reverberant level Gr will be too high, and vice versa. In contrast, if RD has an optimum value, related to the average inter-orchestral distances, transparency and reverberant level will be optimal. On the other hand, RD is not straightforward to measure, and therefore its squared relative, the ratio V/T is a more convenient measure.

Empirical data on the ratio V/T and number of musicians N in ensemble rehearsal rooms provide improved explanation of how well liked the rooms are or not. The important perceptual aspects controlled by V/TN is the relative level and the transparency of the sound field. These two aspects come in entangled pairs, e.g. higher reverberant level & lower transparency, or lower reverberant level & higher transparency. An implication of the result is that the ratio V/T must be planned or adjusted relative to the number of musicians N and the floor space S they occupy. For a symphony orchestra or other ensembles that occupy S/N=1.5m2 per musician, V/T=50N seems to be optimum. This is equivalent to V/TN=50. An implication of these findings is that the observed optimum values are applied as target values. However, targets values must be restricted to the types of ensembles and music from which the data was retrieved. For a choir or a brass band, V/TN=25 and V/TN=100 may be more suitable. This should be explored in further work. It is plausible that acoustic conditions that are good for ensemble rehearsals will also be good for performance with the same ensemble. However, it has been suggested that general rehearsals and performance require less transparency and more orchestral blend than does ordinary rehearsals. This should be investigated in further work.